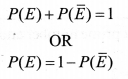Exercise 15.1
Question 1:
Complete the following statements:
(i) Probability of an event E + Probability of the event ‘not E’ = _______.
(ii) The probability of an event that cannot happen is _________. Such as event is called
_________.
(iii) The probability of an event that is certain to happen is _________. Such as event is
called ________.
(iv) The sum of the probabilities of all the elementary events of an experiment is
_________.
(v) The probability of an event is greater than or equal to _______ and less than or equal
to _______.
Answer:
(i) 1
(ii) 0, impossible event
(iii) 1, sure event or certain event
(iv) 1
(v) 0, 1
Question 2:
Which of the following experiments have equally likely outcomes? Explain.
(i) A driver attempts to start a car. The car starts or does not start.
(ii) A player attempts to shoot a basketball. She/he shoots or misses the shot.
(iii) A trial is made to answer a true-false question. The answer is right or wrong.
(iv) A baby is born. It is a boy or a girl
Answer:
(i) It is not an equally likely event, as it depends on various factors such as whether the
car will start or not. And factors for both the conditions are not the same.
(ii) It is not an equally likely event, as it depends on the player’s ability and there is no
information given about that.
(iii) It is an equally likely event.
(iv) It is an equally likely event.
Question 3:
Why is tossing a coin considered to be a fair way of deciding which team should get the
ball at the beginning of a football game?
Answer:
When we toss a coin, the possible outcomes are only two, head or tail, which are equally
likely outcomes. Therefore, the result of an individual toss is completely unpredictable.
Question 4:
Which of the following cannot be the probability of an event?
(A) 2/3 (B) -1.5 (C) 15% (D) 0.7
Answer:
Probability of an event (E) is always greater than or equal to 0. Also, it is always less than
or equal to one. This implies that the probability of an event cannot be negative or
greater than 1. Therefore, out of these alternatives, −1.5 cannot be a probability of an
event.
so our answer is (B) (B is not probability of an event )
Question 5:
If P(E) = 0.05, what is the probability of ‘not E’?
Answer:
We know that,
P(Ē) = 1-P(E)
P(Ē) = 1-0.05
P(Ē) =0.95
therefore , the probability of 'not E' is 0.95..
Question 6:
A bag contains lemon flavoured candies only. Malini takes out one candy without
looking into the bag. What is the probability that she takes out
(i) an orange flavoured candy?
(ii) a lemon flavoured candy?
Answer:
(i) The bag contains lemon flavoured candies only. It does not contain any orange
flavoured candies. This implies that every time, she will take out only lemon flavoured
candies. Therefore, event that Malini will take out an orange flavoured candy is an
impossible event.
Hence, P (an orange flavoured candy) = 0
(ii)As the bag has lemon flavoured candies, Malini will take out only lemon flavoured
candies. Therefore, event that Malini will take out a lemon flavoured candy is a sure
event.
P (a lemon flavoured candy) = 1
Question 7:
It is given that in a group of 3 students, the probability of 2 students not having the
same birthday is 0.992. What is the probability that the 2 students have the same
birthday?
Answer:
Probability that two students are not having same birthday P ( ) = 0.992
Probability that two students are having same birthday P (E) = 1 − P ( )
= 1 − 0.992
= 0.008
Question 8:
A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag.
What is the probability that the ball drawn is (i) red? (ii) not red?
Answer:
(i) Total number of balls in the bag = 8
Probability of getting red ball=`\frac{Number of favourable outcomes}{Number of total Possible outcomes}`
=`\frac3{8}`
(ii) Probability of not getting red ball
= 1 − Probability of getting a red ball
= 1-`\frac3{8}`
=`\frac5{8}`
Question 9:
A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is
taken out of the box at random. What is the probability that the marble taken out will be
(i) red? (ii) white? (iii) not green?
Answer:
Total number of marbles = 5 + 8 + 4
= 17
(i)Number of red marbles = 5
Probability of getting red marbles=`\frac{Number of favourable outcomes}{Number of total Possible outcomes}`
=`\frac5{17}`
(ii) Number of white marble=8
Probability of getting white marbles`\frac{Number of favourable outcomes}{Number of total Possible outcomes}`
=`\frac8{17}`
(iii) Number of green marbles=4
Probability of getting green marbles`\frac{Number of favourable outcomes}{Number of total Possible outcomes}`
=`\frac4{17}`
Probability of not getting a green marble=`1-\frac4{17}=\frac{13}{17}`
Question : 10
A piggy bank contains hundred 50 p coins, fifty ₹ 1 coins, twenty ₹ 2 coins and ten ₹ 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, what is the probability that the coin ?
(i) will be a 50 p coin?
(ii) will not be a ₹ 5 coin?
Solution:
numberof50pcoins=100numberof1₹coins=50numberof2₹coins=20numberof5₹coins=10totalnumberofcoins=180Probabiltyof(50paisacoins)=100180=5090=2545=59Probilityof(not5₹coins)=1−10180=11−10180180−10180=170180=1718
of2₹coins=20n
Question 11.
Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish (see figure). What is the probability that the fish taken out is a male fish?
Solution:
thetotalnumberoffishintank=5+8=13thenumberofmalefishintank=5
theprobabilityofmalefishintankis=513
Question 12.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see figure.), and these are equally likely outcomes. What is the probability that it will point at
(i) 8?
(ii) an odd number?
(iii) a number greater than 2?
(iv) a number less than 9?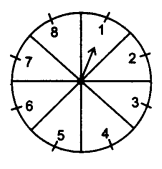
Solution: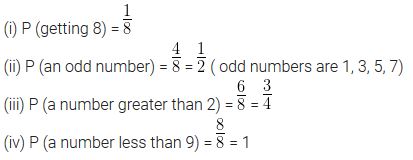
Question 13.
A die is thrown once. Find the probability of getting
(i) a prime number
(ii) a number lying between 2 and 6
(ill) an odd number
Solution:
Class 10 Maths Question 14.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting
(i) a king of red colour
(ii) a face card
(iii) a red face card
(iv) the jack of hearts
(v) a spade
(vi) the queen of diamonds
Solution:
Class 10 Maths Question 15.
Five cards – the ten, jack, queen, king and ace of diamonds, are well shuffled with their face downwards. One card is then picked up at random.
(i) What is the probability that the card is the queen?
(ii) If the queen is drawn and put aside, what is the probability that the second card picked up is
(a) an ace?
(b) a queen?
Solution:
10 Maths Question 16.
12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution:
Ex 15.1 Class 10 Maths Question 17.
(i) A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
(ii) Suppose the bulb drawn in (i) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?
Solution:
Ex 15.1 Class 10 Maths Question 18.
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
(i) a two digit number.
(ii) a perfect square number.
(iii) a number divisible by 5.
Solution:
Ex 15.1 Class 10 Maths Question 19.
A child has a die whose six faces show the letters as given below:
The die is thrown once. What is the probability of getting
(i) A?
(ii) D?
Solution:
Ex 15.1 Class 10 Maths Question 20.
Suppose you drop a die at random on the rectangular region shown in figure. What is the probability that it will land inside the circle with diameter 1 m?
Solution:
Ex 15.1 Class 10 Maths Question 21.
A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that
(i) she will buy it?
(ii) she will not buy it?
Solution:
Ex 15.1 Class 10 Maths Question 22.
Two dice, one blue and one grey, are thrown at the same time. Now
(i) Complete the following table:
(ii) A student argues that-there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability
Solution:
Ex 15.1 Class 10 Maths Question 23.
A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanif wins if all the tosses give the same result, i.e. three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Solution:
Ex 15.1 Class 10 Maths Question 24.
A die is thrown twice. What is the probability that
(i) 5 will not come up either time?
(ii) 5 will come up at least once?
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment.]
Solution:
Ex 15.1 Class 10 Maths Question 25.
Which of the following arguments are correct and which are not correct? Give reasons for your answer.
(i) If two coins are tossed simultaneously there are three possible outcomes- two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is
(ii) If a die is thrown, there are two possible outcomes- an odd number or an even number. Therefore, the probability of getting an odd number is
Solution:
Class 10 Maths Probability Mind Maps
Probability – An Experimental (Empirical) Approach
Let n be the total number of trails. The empirical probability of an event E happening, is given by
(i) Experiment : An operation which can produce some well defined outcomes is known as experiment.
(ii) Trail : Performing of an experiment is called trial.
(iii) Equally likely outcomes : Outcomes of trial are equally likely if there is no reason to accept one in preference to the others.
(iv) Sample space : The set of all possible outcomes of an experiment is called sample space.
(v) Elementary event : An event having only one outcome
Note that the sum of probabilities of all the elementary events of an experiment is 1.
Probability – A Theoretical Approach(Classical Probability)
If an event ‘A’ can happen is ‘m’ ways and does not happen in ‘n’ ways, then the probability of occurrence of event ‘A’ denoted by P(A) is given by
Number of favourable outcomes m
Probability of Impossible and Sure Events
The probability of an event which is impossible to occur is 0 and such an event is called impossible event, i.e; for impossible event T, P(I) = 0
The probability of an event which is sure or certain to occur is 1 and such an event is called sure event or certain event.
i.e; for sure event or certain event ‘s’, P(s) = 1
Range of the Probability of an Event
From the definition of the probability P(E), we see that the numerator (number of outcomes favourable to the event E) is always equal or greater than 0 but less than or equal to the denominator (the number of all possible outcomes). Therefore,
0 ≤ P(E) ≤ 1
Complementary Events
The event representing (‘not E) is called the complement of event ‘E’ and we say that the events E and 